피보나치 파이썬으로 구하는 3가지 알고리즘
피보나치 파이썬 3가지 알고리즘
피보나치 수열은 아래의 수식은 만족하는 수열입니다.
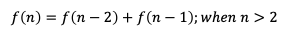
바로 이전 숫자와 그 전 숫자의 합을 연속해서 구하는 수열이고 아래와 같이 진행됩니다.

이번 글에서는 시간 복잡도에 따른 피보나치 수열을 구하는 대표적인 3가지 알고리즘에 대해서 알아보도록 하겠습니다.
- 재귀함수 이용 - 시간복잡도 O(n^2)
- 동적 계획법 이용 - 시간복잡도 O(n)
- 행렬 멱법 이용 - 시간복잡도 O(log n)
재귀함수 이용
첫번 째 방법은 재귀함수를 이용하는 방법입니다.
def fibo(n):
if n in (1,2):
return 1
return fibo(n-1) + fibo(n-2)
print(fibo(8))가장 간단한 방법이지만... 재귀로 두개의 분기가 계속해서 생기기 때문에 시간복잡도가 O(n^2)로 매우 비효율적이다. 피보나치 수열을 구하는 알고리즘 문제를 풀 때... 재귀함수로 풀면 대부분 효율성 테스트는 통과하지 못할 것이다.
동적 계획법 이용
def fibo(n):
cache = [0, 1]
for i in range(2, n+1):
cache.append(cache[i-1] + cache[i-2])
return cache[n]
print(fibo(8))동적 계획법을 사용하면 재귀로 했을 때 중복되는 계산과정을 재사용할 수 있다. 이러면 n까지 한번씩만 계산해주면 문제를 해결할 수 있어 시간 복잡도가 O(n)이 된다. 대부분의 피보나치 알고리즘 문제들은 이정도 효율을 갖고 해결할 수 있지만... 몇몇 문제들에서는 더 큰 범위의 input이 주어지고 더 빠른 알고리즘을 요구하는 문제들이 있습니다. 이런 문제는 행렬 멱법을 통해 해결할 수 있다.
행렬 멱법 이용
행렬 멱법은 점화식을 행렬화 시켜서 푸는 방법 입니다. 행렬 멱법을 자세히 보기 전에... 행렬을 이용해서 시간 복잡도를 O(log N)까지 줄일 수 컨셉은 아래와 같습니다.

행렬의 거듭제곱을 이용하면 우선 시간 복잡도를 O(log n)으로 맞출 수 있습니다. 위의 예시를 봤을 때 8이나 11번째 피보나치 수열의 수를 구한다고 했을 때 동적 계획법을 사용했던 것처럼 N까지 하나씩 모두 계산해보는게 아니라... 절반씩 줄여가면서 계산하기 때문에 시간 복잡도를 O(log n)으로 만들 수 있습니다.
점화식 변형
그렇다면 어떻게???... 행렬을 이용해서 알고리즘을 만들 수 있는 것일까요? 점화식을 이용해서 절차를 보여드리겠습니다.
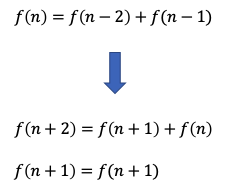
먼저 피보나치의 점화식을 행렬의 곱셉으로 사용하기 위해 변경하면... 그림 2와 같이 두가지 식을 만들 수 있습니다.

그림 2에서 본 두 식을 행렬의 곱셈으로 표현하면 그림 3과 같이 할 수 있습니다. 행렬 형태로 분리하면 다시 함수의 행렬이 나오는데... 이 함수 행렬도 우항의 함수와 같은 형태입니다. 일단 다시 분해를 해보면 아래와 같습니다.

함수 행렬을 다시 분해하면 똑같은 패턴으로 분리가 되면서 최종적으로 사용할 식이 나옵니다.

그림 3과 그림 4의 식을 정리해보면 위의 최종 식으로 정리됩니다. 함수가 들어 있는 행렬의 인자가 1,0이 될 때까지 숫자 형태로 되어 있는 행렬의 거듭제곱을 n만큼 진행합니다.
풀이
위의 풀이 내용을 정리해보면 코드화 시켜야할 부분은 아래와 같습니다.
- 행렬의 거듭제곱
- 짝수와 홀수 일때 차이가 있다.
- 행렬의 멱법
- 숫자 형태의 행렬을 거듭제곱할 수 있도록한다.
- f(1), f(0)값은 각각 1 과 0으로 값이 정해져 있어 곱해주는 작업은 생략하고 행렬 A[0][0] 위치의 값을 반환한다.
- 피보나치 수열은 첫 번째, 두번째 자리가 1로 시작하여 해당 방식으로 할 때는 실제로 함수에 넣는 값에 -1해서 넣는다.
def matrix_mult(A, B):
temp = [[0] * 2 for _ in range(2)]
for i in range(2):
for j in range(2):
for k in range(2):
temp[i][j] += (A[i][k] * B[k][j])
return temp
def matrix_pow(n, M):
if n == 1:
return M
if n % 2 == 0:
temp = matrix_pow(n//2, M)
return matrix_mult(temp, temp)
else:
temp = matrix_pow(n-1, M)
return matrix_mult(temp, M)
A = [[1, 1], [1, 0]]
print(matrix_pow(8-1, A)[0][0])행결의 곱셉 작업을 할 수 있는 matrix_mult 함수와 M의 n제곱을 구할 수 있는 matrix_pow함수를 이용해서 행렬을 이용한 피보나치 수열을 구할 수 있다. 해당 방법으로 하면 시간 복잡도를 O(log n)까지 줄일 수 있어 다루는 숫자의 범위가 커질수록 매우 큰 효율을 얻을 수 있다.